What Is the Significance of Blue Values in Decision Tree

Understanding Decision Trees (once and for all!) 🙌

Photo by David Vig on Unsplash

This article is made for complete beginners in Machine Learning who want to understand one of the simplest algorithm, yet one of the most important because of its interpretability, power of prediction and use in different variants like Random Forest or Gradient Boosting Trees.
This article is also for all the Machine Learners like me who rushed towards the children of Decision Trees (Random Forest or Gradient Boosting Trees), because they usually performed better at Kaggle competition, forgetting to get familiar with the Decision Trees and unveiling all its mystery. 🔮

The first part of the article is about setting up the dataset and model, the second part is about understanding the model : the Decision Tree.

This article is also coupled with a notebook that you can find here.

Setting up the dataset and the model

Defining the objective

Iris sepal and petal

To demystify Decision Trees, we will use the famous iris dataset. This dataset is made up of 4 features : the petal length, the petal width, the sepal length and the sepal width. The target variable to predict is the iris species. There are three of them : iris setosa , iris versicolor and iris virginica .

Iris species

First thing we can notice is that for a non expert in gardening like me, it is quite difficult to distinguish the difference between these three iris species. Let's use Machine Learning to do this task ! 😃

Analysing the dataset

Now that we know what we are looking for let's take a closer look at the dataset.

First 10 rows of the iris dataset

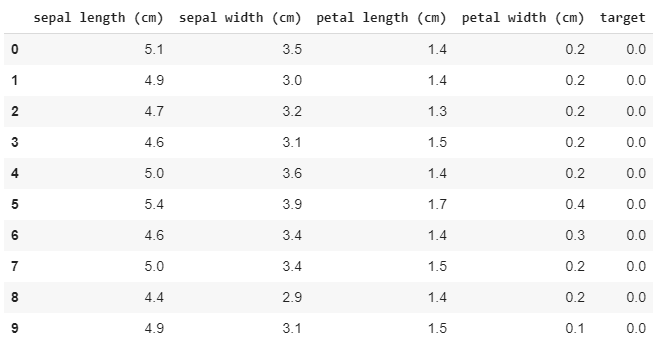
On the picture above we can see the first 10 rows of the iris dataset. The first 4 columns are the first 4 features that we will use to predict the target, the iris species, represented by the last column with numerical values : 0 for setosa, 1 for versicolor, 2 for virginica.
In total, we have 150 observations (150 rows), 50 observations for each iris species : the dataset is balanced.

Preparing the dataset and feature selection

To ease our understanding of how a Decision Tree works we will only work on two features : petal width and sepal width. (We then remove observations where there are duplicates for these features to be able to see every point on the graphs that we will plot to help our understanding).

Modeling and Evaluating

As you will have understood, the model chosen is a…

…DECISION TREE !!! 😉

Without optimizing the hyperparameters (like the tree depth, minimum number of leaves in a node or to split a node…) and with only two features we already obtain 93% of accuracy on the testing set.

Accuracy is the number of good predictions over the number of predictions.

This metric is interesting but does not help us understand what the Decision Tree gets wrong. The confusion matrix can help us.

Confusion matrix of the Decision Tree on the testing set

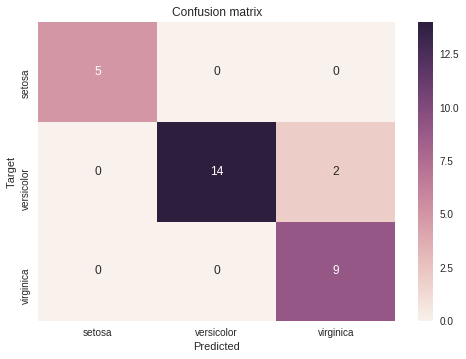
The confusion matrix above is made up of two axes, the y-axis is the target, the true value for the species of the iris and the x-axis is the species the Decision Tree has predicted for this iris. On the top-left square we can see that for the 5 setosa irises, the Decision Tree has predicted setosa for the species. The second line shows that out of 16 versicolor irises 14 have been classified as versicolor and 2 have been mistaken for virginica. This is the reason why we don't have a 100% accuracy. Finally the bottom-right square shows that all the virginica irises have been classified as virginica.
Thanks to the confusion matrix we can retrieve the accuracy : all the diagonal elements are the good predictions, 5+14+9=28, and all the predictions is all the squares, 5+14+2+9=30. We find the same accuracy 28/30 = 93%.

Understanding how the Decision Tree was built

Now that we have set up our dataset and model we can dive into the construction of a Decision Tree, finally ! 😜

Visualizing the tree

Decision Tree built after training

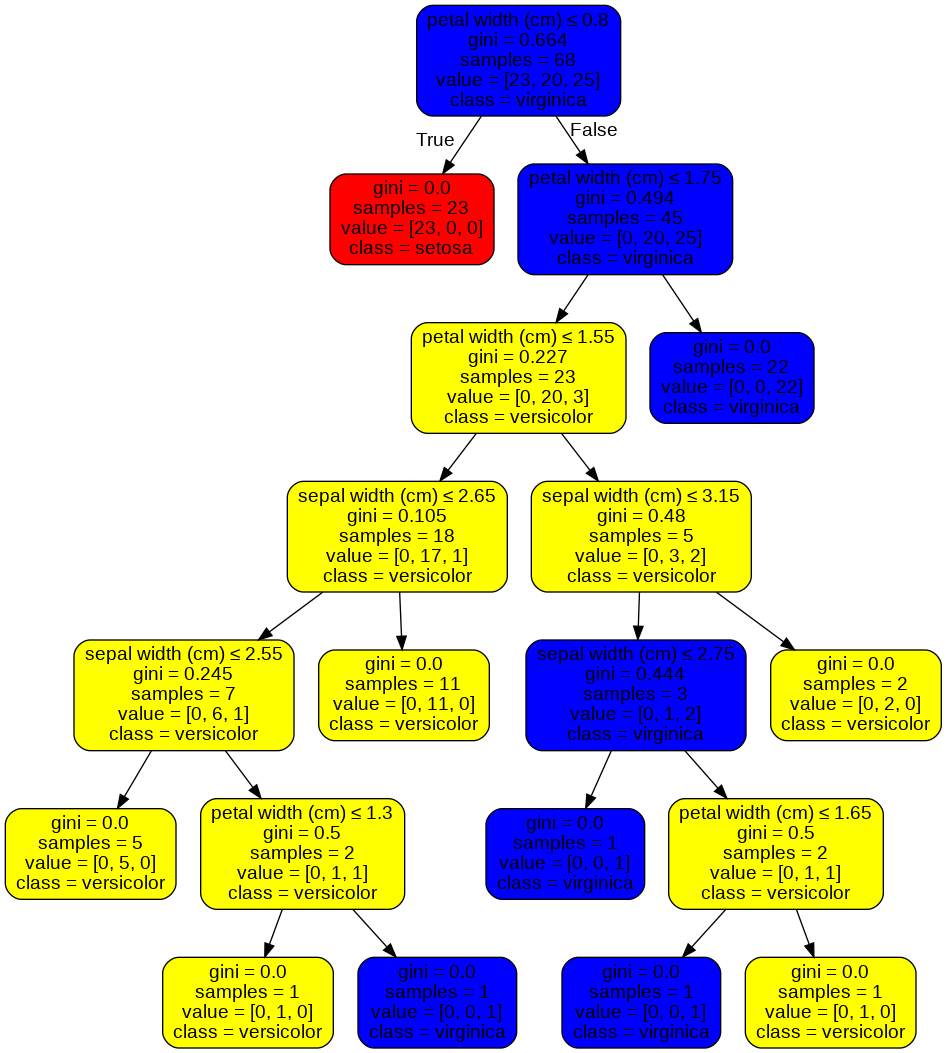
Above we can see the tree built after training. During the training phase, the Decision Tree add nodes, split them into branches that lead to leaves.

How do we obtain this tree ? 🌳

The tree is built iteratively from the root to the the leaves thanks to the training set. Indeed, the dataset is split into two : the training set that the Decision Tree is using to train itself and the testing set used to measure the performance of the Decision Tree once built by comparing its predictions to the real values.

The goal of a Decision Tree is to split the training set into homogeneous areas where only one iris species is present according to the features given : here the petal and sepal widths.

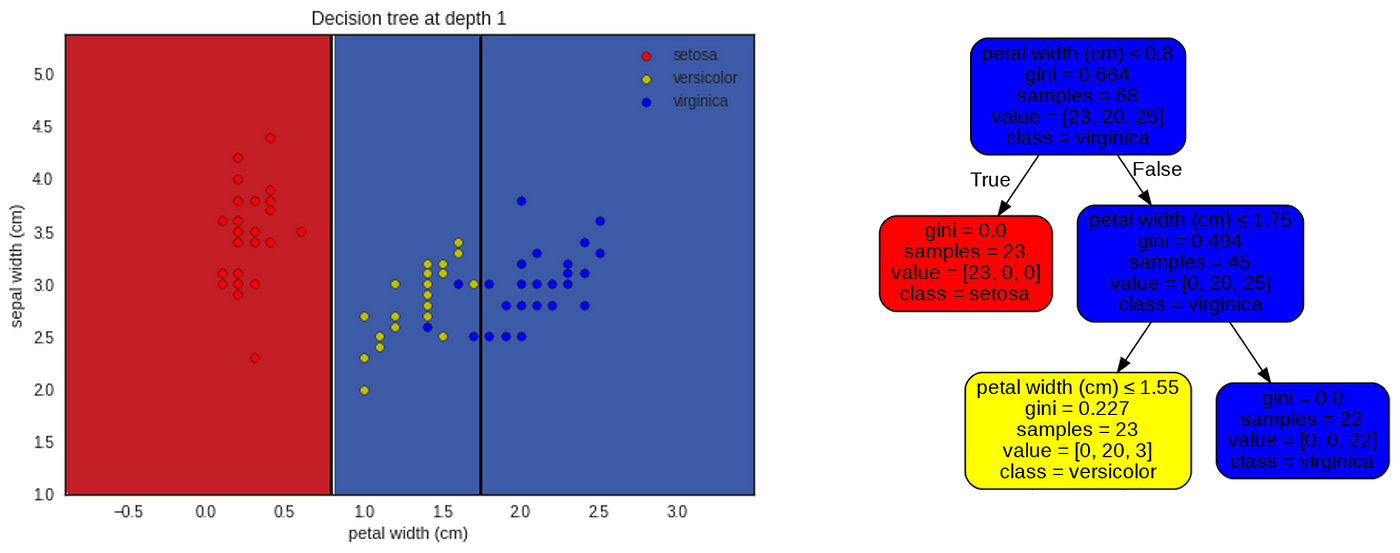
Node 0 : Root node

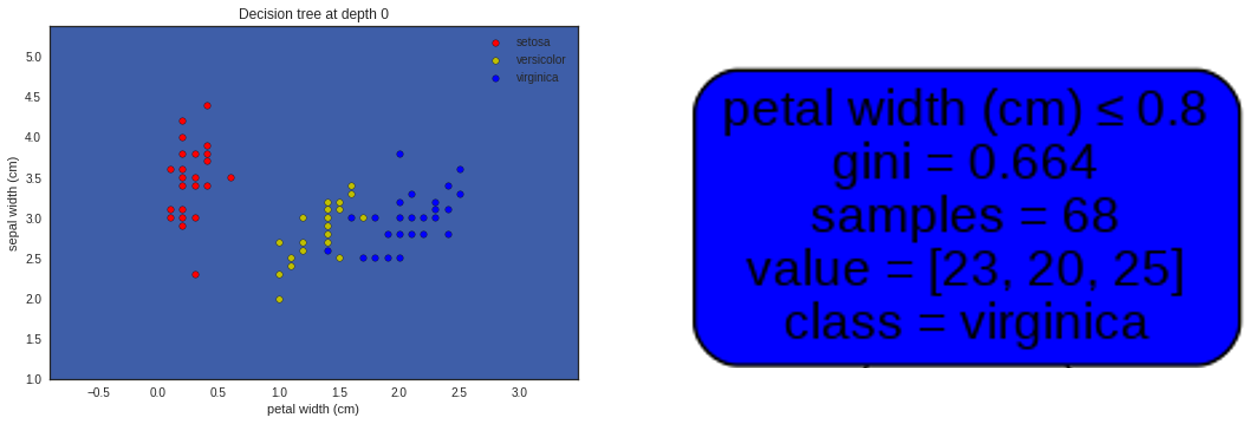
The graph above shows the distribution of iris species according to the two features selected : petal width on the x-axis and sepal width on the y axis. The color of the dots represents the iris species : red for setosa, yellow for versicolor, blue for virginica.
The root node, on the right of the picture above, gives us several information :
- There are 68 irises ('samples=68'), irises dots that we can count on the plot on the left;
- 'value=[23,20,25]' describes the repartition of these irises among the tree possible classes of iris species, i.e. 23 for the setosa, 20 for the versicolor, and 25 for the virginica;
- 'class = virginica'. This is the iris species predicted by the Decision Tree at the root node. This decision is taken because virginica is the most numerous species at the root node (25 virginica compared to 20 versicolor and 23 setosa). This is the reason why the background color on the left graph is blue, the color chosen for the virginica species.
The root node also gives us two more pieces of information 'petal width (cm) ≤ 0.8' and 'gini = 0.664'. We will discuss what they mean now… 😃

Node 0: let the learning begin ! 😎

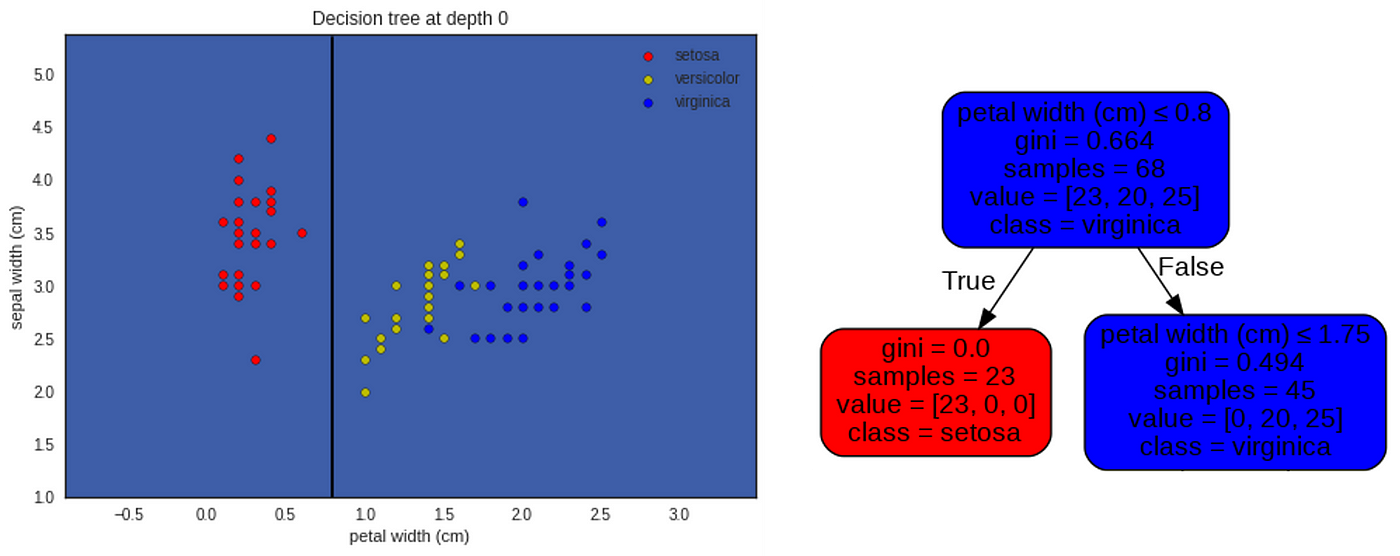
This plot on the left is the same as the previous one but with the first decision boundary of the tree : petal width = 0.8 cm .

How was this decision boundary decided ?

A decision boundary is decided by testing all the possible decision boundaries splitting the dataset and choosing the one that minimizes the Gini impurity of the two splits.

What is Gini impurity ?

Gini impurity is a metric that measures the probability from a randomly chosen element (here an iris) to be incorrectly classified, i.e. the probability of choosing an element times the probability of being misclassified. If we sum over all J possible classes we have the Gini impurity :

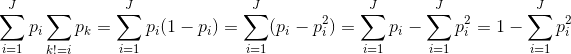
The last expression is the one we are going to use to perform the Gini test.

Let's compute the Gini impurity for the first node

At the root node all the data points are mixed. Using the result above Gini impurity is :

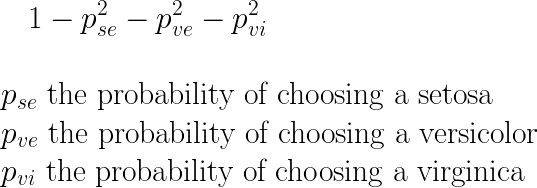
This gives us :

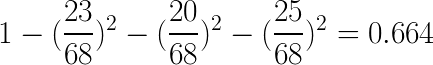
We can verify this number by checking the Gini information on the root node : 'gini = 0.664'. For the first node we have a Gini impurity of 0.664.

Let's get back to the first decision boundary

The question to be asked to determine a decision boundary is : how to split the iris species so that we create more homogeneous groups ?
Intuitively what we can observe on the graph above is that we can create a homogeneous group containing only setosa species just by splitting the dataset along the petal width axis.

But the algorithm has no intuition. So how does it find the best split ?

• It will try all the possible boundaries along all the features, i.e. all the axes petal width and sepal width.
• For each split the algorithm will compute the Gini impurity of the two groups created.
• Finally it will choose the decision boundary that gives the lowest Gini impurity for the two groups (either summing the Gini impurity for each group or doing a mean).

Let's get back to the first node and the first split

In the case of the root node, the algorithm has found that among all the possible splits the split with petal width = 0.8 cm gives the lowest Gini impurity.
The Gini impurity for the left leaf is :

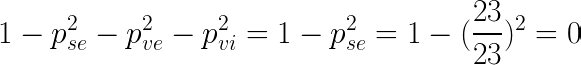
We verify this result with the tree graph. This result is not surprising because in the left leaf which matches the left part of the graph we only have setosa iris, so the group is very homogeneous and Gini impurity is a measure of homogeneity.

The Gini impurity for the right leaf is :

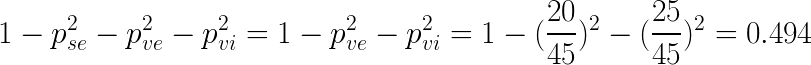
We find the same result as the one shown in the tree graph. Moreover this Gini impurity is close to 0.5 because there are almost as much virginica as versicolor irises.

Node 1

The process described will continue iteratively until the tree succeeds or tries to separate all the data points or a restrictive condition is applied to the algorithm like a limitation in the depth of the tree.

As the Gini impurity is 0 for petal width <= 0.8 cm , i.e. we cannot have a more homogeneous group, the algorithm will not try to split this part anymore and will focus on the right part of the tree.

Intuitively, the decision tree continues to use the petal width feature to split the right part in two. Indeed, it seems easier to create homogeneous groups using petal width instead of sepal width. Splitting at petal width <= 0.8 cm creates a group with only virginica irises (so with a Gini impurity of 0). Managing to create a group with uniquely one species is not always the best option though, as we will see for the next split…

As the algorithm has created a node with only virginica, this node will never be split again and it will be a leaf.

Node 2

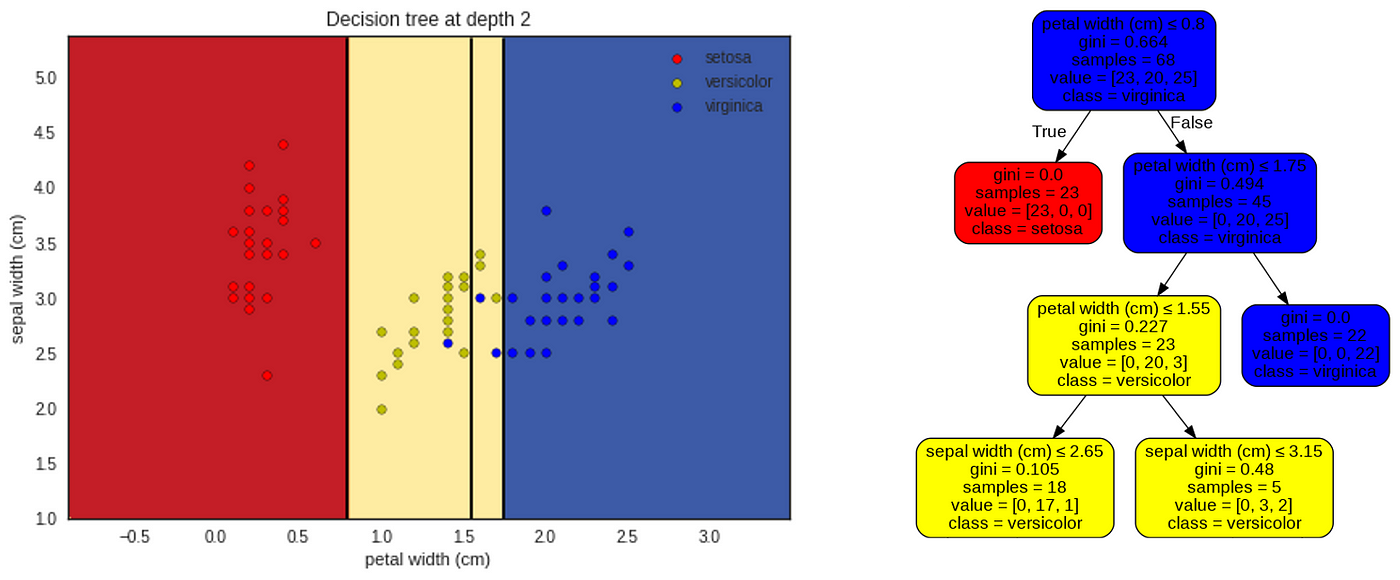
For this node the algorithm chose to split the tree at petal width = 1.55 cm creating two heterogeneous groups. Intuitively we would have split at petal width = 1.3 cm or sepal width = 3.1 cm to create a group with only versicolor irises. Indeed this would have created a node with a Gini impurity at 0. But in fact the other node created is more heterogeneous, so much so that the Gini impurity of this node is bigger than the Gini impurity of the sum of the two nodes created with the other split.

Let's verify this :

Gini impurity with the split at petal width = 1.55 cm

• Left node :

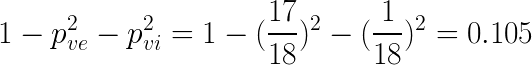
We verify this result on the tree.

• Right node :

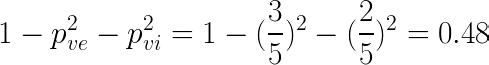
Again we verify this result on the tree.

• The Gini impurity for this split is :

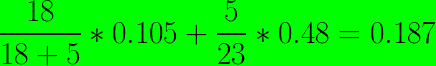
The Gini index of a split is ponderated by the number of points for each group.

Gini impurity with the split at petal width = 1.3 cm

• Left node :

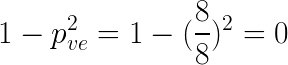
• Right node :

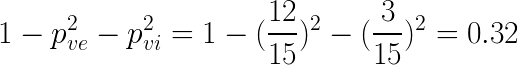
• The Gini impurity for this split is :

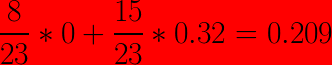
The algorithm is right and our intuition was wrong. Indeed the first split produces the lowest Gini impurity so this split is preferable. Reminder : The algorithm tries each possible split for each feature.

Node 3

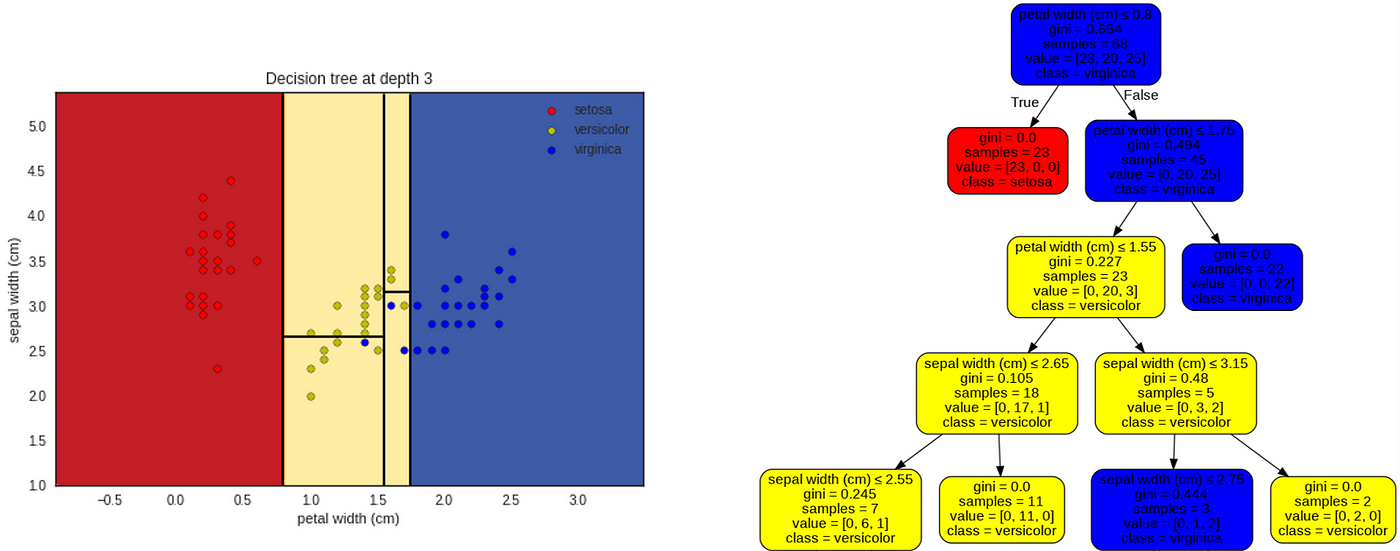
The first thing to notice is that the previous split has not changed the decision function of the tree below and above the split petal width = 1.55 cm . Indeed for both nodes created, the versicolor still holds the majority.

For this level, the decision tree finally uses the sepal width feature. The two splits created are petal width = 2.65 cm (in the subdivision 0.8 cm < petal width <= 1.55 cm ) and petal width = 3.15 cm (in the subdivision 1.55 cm < petal width <= 1.75 cm ).

Nodes 4, 5, 6

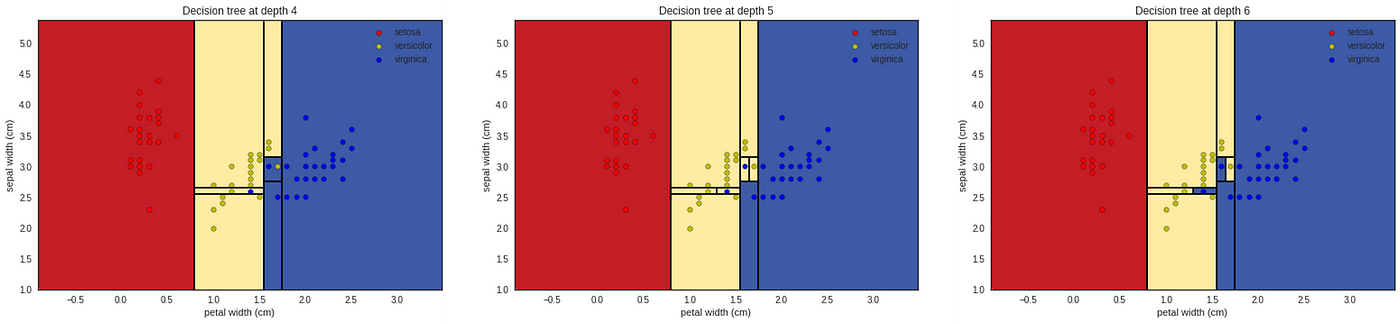
Applying the same principle again and again the algorithm will try to isolate every point until it has only homogeneous groups. This can lead to overfitting if we don't limit the size of the tree for example. (The tree is learning by heart the training set instead of understanding it which will prevent him from making good predictions on the testing set).

On the graph above we can see the decision boundaries being decided for the tree at depth 4, 5, 6. The depth 6 is the depth of leaves and ends the building of the tree.

How does the built tree take a decision ?

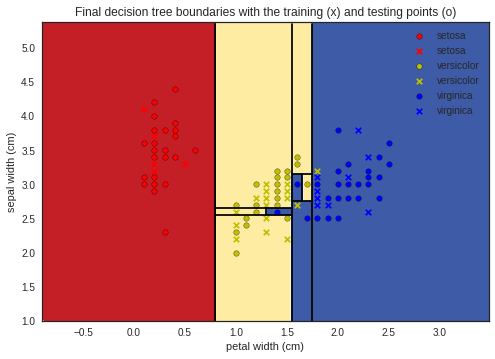
On the plot above we can see the training data (represented by o) on which the Decision Tree has been trained (and has overfitted) and the the testing data (represented by x).

When the Decision Tree has to predict a target, an iris species, for an iris belonging to the testing set, it travels down the tree from the root node until it reaches a leaf, deciding to go to the left or the right child node by testing the feature value of the iris being tested against the parent node condition.

For example, at the root node if the tested iris petal width <= 0.8 cm it goes to the left node which is a leaf and classifies the iris as a setosa iris. Otherwise, it goes to the right node and continues the same process until reaching a leaf.

As we have seen with the confusion matrix, two versicolor have been misclassified for virginica :

• in the region 1.75 cm < petal width : we can see the yellow cross, i.e. it is a versicolor iris, on the blue background, i.e. the Decision Tree classifies it as a virginica.
• in the region 1.55 cm < petal width <= 1.75 cm and sepal width <= 2.75 cm : it is the same reasoning as above.

The rest of the testing irises have been well classified which gives us an accuracy of 0.93.

During the testing phase, the algorithm takes every point and travels across the decision tree choosing the left or right node according to the feature value of the iris being tested.

Conclusion

In this article, we dissected Decision Trees to understand every concept behind the building of this algorithm that is a must know. 👏
To understand how a Decision Tree is built, we took a concrete example : the iris dataset made up of continuous features and a categorical target. Decision Trees can also be built using categorical features (it is even simpler because one branch is one category) or a continuous target (here it may be a bit more complex because it does not use Gini impurity to measure the homogeneity but a variance metric…). This could be the subject of another article…

isaacbegarly1971.blogspot.com

Source: https://towardsdatascience.com/understanding-decision-trees-once-and-for-all-2d891b1be579

Share this post